Jue Yan advances mathematical models for research simulations

CATEGORIES: Math Matters, Math Matters 2016
Jue Yan performing mathematical computations at a blackboard.

Could you multiply 26 by 24 instantly as a child? Jue Yan could.

Growing up, Yan, now an associate professor in the Department of Mathematics at Iowa State University, learned many interesting math tricks from her father.

“I grew up with a strong curiosity,” Yan said. “Solving a hard problem was always a rewarding and happy moment for me. Over the last 10 years of my research in applied mathematics, I have become more and more fascinated by the world of math. Finding a new idea to conquer a difficult problem still excites me the most.”

Today Yan researches the design, analysis, and implementation of numerical methods that solve partial differential equations arising from physics and engineering.

With the development of modern computers, numerical simulation has become a major tool to study physical phenomena due to increased speed and decreased cost compared to a traditional lab experiment. Numerical simulation uses algorithms, or sets of calculation processes, to numerically simulate the physical phenomena that would be produced in a lab experiment. Yan works on developing and improving these algorithms to give more accurate and precise data.

Yan recently received a grant from the National Science Foundation for her research into numerical methods guaranteed to give solutions in a given range without losing accuracy.

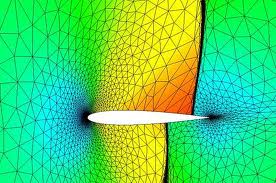
Computer image of computational meshes around a cross section of an airplane wing.
Cut-off 2-dimensional look at the wings and
the computational meshes used around the wing.
“Dr. Yan has become one of the foremost authorities in her field,” said Clifford Bergman, professor and chair of the Department of Mathematics. “With this grant she will apply her considerable analytical skills to new problems in numerical methods.”

Yan’s research on bounding the data can make simulations more robust and consistent with physical meaning.

Computer image of an airplane with mesh around it and heat map coloring.
An airplane with meshes around it.
For example, aerospace engineers need to calculate the lifting and dragging forces around fast flying objects, such as airplane wings. In these situations air density can be very low, near zero, or vacuum, conditions. When the density is this low, simulated models can easily yield calculations that show a negative air pressure — an impossible situation. Yan’s methods focus on eliminating these impossible negative results, producing more accurate data from the simulations.

“There are still many challenging problems that need to be conquered by applied mathematicians before the computational algorithms are built into the industrial simulation software,” Yan said.

Bounding outcomes is also useful in bio-chemical applications, such as in the Keller-Segel chemotaxis equations. The Keller-Segel system is a mathematical model to effectively describe chemotaxis, the directional movements of cells in response to a chemical stimulus, an important component of immune system responses, tumor metastasis, wound healing, and blood vessel formation. Yan’s method of bounding outcomes ensures a positive cell density approximation in simulations, eliminating impossible negative cell density outcomes.

Yan’s work shows the important role that mathematics plays in modern science to develop and verify mathematical models for continued advancements in fields ranging from engineering to medicine.

By Elizabeth Peterson

Published: January 7, 2017